TRIGONOMETRY:SINE, COSINE AND AREA RULES QUESTIONS AND ANSWERS GRADE 12 Trigonometry is a branch of mathematics that focuses on relationships between the sides and angles of triangles. The word trigonometry comes from the Latin derivative of Greek words for triangle (trigonon) and measure (metron).
Activity 1
In triangle ABC, ^B = 37° and AC = 16 cm. ^C = 90°. Calculate the length of AB and BC (correct to one decimal place). (3)

| Solution To calculate the length of AB, use 37° as the reference angle, then AC = 16 cm is the opposite side and AB is the hypotenuse. Use the sine ratio. sin 37° = opp =16 hyp AB AB sin 37° = 16 AB = 16 = 26,6 cm sin37° To find the length of BC, you can use cos 37° = adj = BC/26.6 hyp 26,6 cos 37° = BC BC = 21,2 cm (to one decimal place) You can also use Pythagoras’ theorem: AB2 = AC2 + BC2 [3] [3] |
Activity 2
In triangle PQR, PQ = 12,3 m and PR = 13 m. Calculate the size of ^Q . (2)

[2]
| Solution Use PQ and PR. tan θ = opp = 13 12.3 θ = tan–1 (13/12.3) = 46,58° [2] |
Activity 3
Solve ∆XYZ in which z = 7,3 m, ^X = 43° and ^Y = 96°. Give your solutions correct to 3 decimal places. (4)

[4]
| Solution The angle opposite the known side is not given, but you can work it out. ^Z = 180° – (43° + 96°) (sum angles of ∆) ^Z = 41° To find y: y = 7,3 sin 96° sin41° y = 7,3 sin 96° sin41° y = 11,066 m Using the sine rule again to find x: x = 7,3 sin43° sin41° x = 7,3 sin 43° sin41° x = 7,589 m [4] |
Activity 4
1. PQRS is a trapezium with PQ // SR, PQ = PS, SR = 10 cm,
QR = 7 cm, ^R = 63°.

Calculate:
- SQ (2)
- PS (6)
- area of quadrilateral PQRS. (correct to 2 decimal places) (5)
[13]
Solutions
|
When solving triangles, start with the triangle which has most information (i.e. triangle with three sides or two sides and an angle or two angles and a side given)
Activity 5
In the diagram alongside, AC = 7 cm,
DC = 3 cm, AB = AD, DCA = 60°,
DAB = β and ABD = θ.
Show that BD = √37 sin β
sinθ

[3]
| Solution AD2 = AC2 + CD2 − 2AC.CD cos 60 ° = (7)2 + (3)2 – 2 × 7 × 3 × 0,5 AD2 =58 – 21 AD2 = 37 AD = √37 P Applying sine rule: BD = AD ⇒ BD = AD sin β but AD = √37 sinβ sinθ sinθ ∴BD = √37 sin β sinθ [3] |
Activity 6
- In the diagram alongside, ABC is a right angled triangle. KC is the bisector of ACB. AC = r units and BCK = x
1.1 Write down AB in terms of x (2)
1.2 Give the size of AKC in terms of x (2)
1.3 If it is given that AK = 2 , calculate the value of x (7)
AB 3
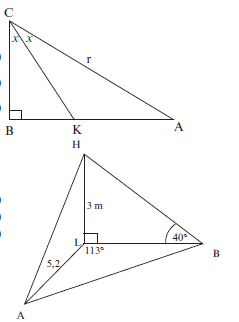
- A, B and L are points in the same horizontal plane, HL is a vertical pole of length 3 metres,
AL = 5,2 m, the angle ALB = 113° and the angle of elevation of H from B is 40°.
2.1 Calculate the length of LB. (3)
2.2 Hence, or otherwise, calculate the length of AB. (3)
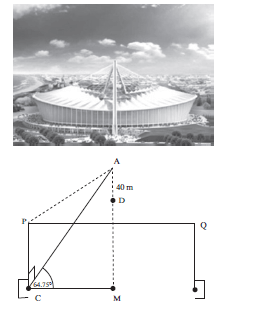
2.3 Determine the area of ∆ABL. (3) - The angle of elevation from a point C on the ground, at the centre of the goalpost, to the highest point A of the arc, directly above the centre of the Moses Mabhida soccer stadium, is 64,75°. The soccer pitch is 100 metres long and 64 metres wide as prescribed by FIFA for world cup stadiums. Also AC ⊥ PC.
In the figure below PQ = 100 metres and PC = 32 metres
3.1 Determine AC (2)
3.2 Calculate PAC (2)
3.3 A camera is placed at D, 40 m directly below point A, calculate the distance from D to C (4)
[28]
| Solutions 1.1 sin 2x = AB ∴ AB = r sin 2x (2) r 1.2 AKC = 90° + x [ext. angle of ∆CBK] (2) 1.3 AK = r ∴ AK = r sinx sin x sin(90° + x) cos x r sin x AK = cos x = r sin x = 1 = 2 AB r sin 2x r cos x.2 cos x sin x 2 cos2x 3 ∴ cos2x = 3/4 cos x = √3/2 Hence x = 30º (7) 2.1 In ∆HLB, tan 40° = 3 LB [∆HLB is right-angled, so use a trig ratio] LB = 3 tan40º LB = 3,5752… ≈ 3,58 metres (3) 2.2 In ∆ABL, [ΔABL not right-angled. You have two sides and included angle, so use the Cosine Rule] AB2 = AL2 + BL2 – 2(AL)(BL).cos L AB2 = (5,2)2 + (3,58)2 – 2(5,2)(3,58).cos 113° AB2 = 54,40410… m2 AB = 7,38 m (3) 2.3 Area ∆ABL = ½ AL × BL × sin ALB = ½ (5,2) × (3,58) × sin 113° = 8,56805… ≈ 8,57 m2 (3) 3.1 cos 64,750° = CM ∴ AC = CM = 50m = 117,21 (2) AC cos64.75° 0.426569 3.2 tanPAC = PC AC PAC = tan−1 (32/AC) = 15,27° (2) 3.3 DC2 = AC2 + AD2 − 2AC.ADcos(90° − 64,75°) DC2 = (117,21 )2 + (40)2 − 2(117,21).40cos(25,25°) = 6857,289 DC = 82,81m (4) [28] |

