ALGEBRA QUESTIONS AND ANSWERS GRADE 12 Algebra is the branch of mathematics in which abstract symbols, rather than numbers, are manipulated or operated with arithmetic. For example, x + y = z or b – 2 = 5 are algebraic equations, but 2 + 3 = 5 and 73 * 46 = 3,358 are not.
Activity 1
Factorise each of the following completely:
- 12x2 + 17x + 6
- 5x2 – 23x – 10
- 9x2 + 5x – 4
- 12x2 – 11x + 2
- 5x2 – 45
- 2x3 + 16
- 6x3 – 13x2 + 5x
[16]
Solutions- 12x2 + 17x + 6
= 12x2 + 9x + 8x +6………..12 × 6 = 72 and 72 = 9 × 8 (9 + 8 = 17)
= 3x(4x + 3) + 2(4x + 3)
= (4x + 3)(3x + 2) (2) - 5x2 – 23x – 10
= 5x2 – 25x + 2x – 10…………5 × –10 = –50 and 50 = 25 × 2 (–25 + 2 = –23)
= 5x(x – 5) + 2(x – 5)
= (x – 5)(5x + 2) (2) - 9x2 + 5x – 4
= 9x2 + 9x – 4x – 4…………..9 × –4 = –36 and 36 = 9 × 4 (9 – 4 = 5)
= 9x(x + 1) – 4(x + 1)
= (x + 1)(9x – 4) (2) - 12x2 – 11x + 2
= 12x2 – 3x – 8x + 2…………..12 × 2 = 24 and 24 = 8 × 3 (–8 – 3 = –11)
= 3x(4x – 1) – 2(4x – 1)
= (4x – 1)(3x – 2) (2) - 5x2 – 45……………………….Common factor of 5
= 5(x2 – 9) ……………………….Difference of two squares
= 5(x – 3)(x + 3) (2) - 2x3 + 16……………………….Common factor of 2
= 2(x3 + 8) ……………………….Sum of two cubes
= 2(x + 2)( x2 – 2x + 4) (3) - 6x3 – 13x2 + 5x……………………….Common factor of x
= x(6x2 – 13x + 5) 3……………………….Trinomial factorising
= x(6x2 – 3x – 10x + 5) ………….. 6 × 5 = 30 and 30 = 10 × 3 (–3 – 10 = –13)
= x[3x(2x – 1) – 5(2x –1)]
= x[(2x – 1)(3x – 5)] (3)
[16]
|
Activity 2
Solve for x:
- x(x + 3) = 0
- x(2x – 5) = 12
- 2x2 + x − 6 = 0
- 2x2 = 32
- 3x + 1/x = 4, x ≠ 0
- 2√x − 3 = x − 3
[22]
If (A) × (B) = 0, then either A = 0 OR B = 0.
Solutions- x(x + 3) = 0 We have a product = 0. Therefore put each factor = 0
x = 0 or x + 3 = 0
x = 0 3 or x = –3 (2) - x(2x – 5) = 12 We need a product = 0. Therefore, multiply out brackets and write in standard form with all the terms on one side and equal to 0
(2x + 3)(x – 4) = 0 Factorise
2x + 3 = 0 or x – 4 = 0 Put each factor = 0
2x = –3 or x = 4
x = -3/2 x = 4 (2) - 2x2 + x − 6 = 0
(2x − 3)(x + 2) = 0 33
∴ 2x = 3 or x = − 2 Find the solutions by putting each factor equal to zero
∴ x = -3/2 or x = −2 (4) - 2x2 = 32
2x2 – 32 = 0 Write in standard form with all the terms on one side and equal to 0
x2 – 16 = 0 Divide every term on both sides by 2
(x + 4)(x – 4) = 0 3 Factorise (the difference of two squares)
∴ x + 4 = 0 or x – 4 = 0
∴ x = –4 or ∴ x = 4 (4) - 3x + 1/x = 4, x ≠ 0 Multiply through by x to get rid of the denominator
3x2 + 1 = 4x Write in standard form with all the terms on one side and equal to 0
3x2 – 4x + 1 = 0 Factorise (the trinomial)
(3x – 1)(x – 1) = 0
∴ 3x – 1 = 0 or x – 1 = 0
∴ 3x = 1 or x = 1
∴ x = 1/3 or ∴ x = 1 (5) - 2 √x − 3 = x − 3 Square both sides
(2 √x − 3)2 = (x − 3)2
4(x − 3 ) = ( x − 3 ) ( x − 3 )
4x − 12 = x2 − 6x + 9
0 = x2 − 10x + 21
0 = ( x − 7 ) ( x − 3 )
∴ x − 7 = 0 or x − 3 = 0
∴ x = 7 or x = 3 (5)
[22]
|
Check your answers:
x = 7
LHS = 2 √7 − 3 = 2 √4 = 2(2) = 4 RHS = 7 − 3 = 4 ∴ x = 7 is a solution
x = 3
LHS = 2 √3 − 3 = 2 √0 = 0 RHS = 3 − 3 = 0 ∴ x = 3 is a solution
If a quadratic equation cannot be factorised, there are other ways to find the roots or solutions. Sometimes the solutions do not exist!
Activity 3
- What term can be added to the following equations to make a complete square?
- 0 = x2 – 8x + ?
- y = x2 + 9x + ?
- y = x2 -b/a x + ?
- Solve for x by using the method of completing the square.
- –3x2 + 5x + 4 = 0
- ax2 + bx + c = 0 [17]

Activity 4: Interpret a graph
Solve for x (correct to two decimal places):
4x2 – 8x = 7
2x (3x + 5) – 11 = 0 [9]
Solutions
1. 4x2 – 8x = 7 Write the equation in standard form (ax2 + bx + c = 0)
4x2 – 8x = 7 = 0 List the values of a, b and c
a = 4; b = – 8; c = –7 Write down the formula
x = − b ± √b2 − 4ac Substitute the values for a, b and c into the formula.
2
x = – ( –8 ) ± √(–8 ) 2 – 4(4)(–7) Simplify the value under the square root sign
2(4)
x = 8 ± √176 Separate the positive and negative value of the square root
8
x = 8 + √176 or x = 8 – √176 Answers in surd form
8 8
x = 2,66 3 or x = –0,66 3 Answers correct to two decimal places (5)
2. 2x(3x + 5) – 11 = 0 Write the equation in standard form
6x2 + 10x – 11 = 0 (ax2 + bx + c = 0)
x = –10 ± √100 + 26
12
= –10 ± √364
12
= –5 ± √91
6 (4)
[9]
These roots are irrational. Unless the question asks for decimal values,
leave them in surd form (the square root form).
|
Activity 5
Solve for x if
- (x+3)(x – 5) ≤–12
- –x ≤ 2x2 – 3 [10]
Solutions- (x+3)(x – 5) ≤ –12
x 2 – 2x – 15 +12 ≤ 0 Get into the standard form (ax2 + bx + c ≤ 0)
x 2 – 2x –3 ≤ 0 3
Factorise the trinomial:
(x –3)(x + 1) ≤ 0 3
Critical values:
x = 3 and x –1
We now indicate 3 and –1 on a number line.
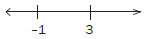
We know that the expression x2 – 2x –3 = 0 at x = 3 and x = –1. We can indicate this on the number line.
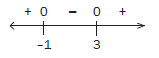
Our next step is to choose values less than –1, values between –1 and 3 and values greater than 3 and substitute it into the expression x 2 – 2x –3. If the answer is positive, then we indicate + on the number line. If the answer is negative, we indicate – on the number line
(If x = –10, then 2(–10)² +(–10) – 3 = 187 > 0 ∴ +
If x = 0, then 2(0)² – 0 –3 = –3 < 0 ∴ –
If x = 3, then 2(3)² + 3 – 3 = 18 > 0 ∴ +)
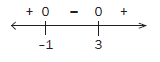
We have to solve for x where x2 – 2x –3 ≤ 0. The solution on the number line is the interval where we see zero and a negative. This happen when the x values are less than or equal to 3 and are also more than or equal to –1.
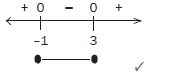
Therefore the solution is : − 1 ≤ × ≤ 3 (5) - –x ≤ 2x2 – 3
–2x2 – x + 3 ≤ 0 Get into the standard form (ax2 + bx + c ≤ 0)
–2x – x + 3 ≥ 0
-1 -1 -1 -1
Divide both sides by –1 to change the coefficient of x2 to a positive
2x2 + x – 3 ≥ 0 3 Factorise the trinomial
(2x + 3)(x – 1) ≥ 0 3
Critical values:
x = –3/2 and x = 1
We now indicate –3/2 and 1 on a number line.
We know that the expression 2x2 + x – 3 = 0 at x = –3/2 and x = 1.
We can indicate this on the number line.
Our next step is to choose values less than –3/2, values between–3/2 and 1 and values greater than 1 and substitute it into the expression 2x2 + x – 3. If the answer is positive, then we indicate + on the number line. If the answer is negative, we indicate – on the number line
(Whenever we multiply or divide an inequality by a negative, the inequality sign changes i.e. the less or equal to sign changes to a greater or equal to sign.
If x = –10, then (–10)² 2(–10) – 3 =117 > 0 ∴ +
If x = 1, then (1)² – 2(1) – 3 =–4 < 0 ∴ –
If x = 5, then (5)² –2(5) – 3 = 12 > 0 ∴ +)
We have to solve for x where 2x2 + x – 3 ≥ 0. The solution on the number line is the interval where we see zero and a positive. This happens for the x values less than or equal to –3/2 and for the x values greater than or equal to 1.
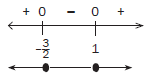
Therefore the solution is : x ≤ − –3/2 or x ≥ 1 33 (5)OR ALTERNATIVE METHOD by using a rough sketch of the parabola:
–x < 2x2 – 3 Get into the standard form ax2 + bx + c < 0
–2x2– x + 3 < 0 Divide both sides by –1.
–2x – x + 3 > 0 This is necessary to draw the rough sketch of a “positive” parabola
-1 -1 -1
2x2 + x – 3 > 0 3 With 0 on RHS
(2x + 3)(x – 1) > 0 3 Factorise LHS
Critical values of x: –3/2 and = 1 Make a rough sketch of a parabola
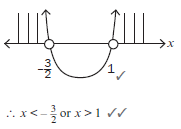
If (***)(***) > 0 (it means where y is positive)
Read off the x values of the graph above the x-axis (5)
[10]
|
Activity 6
Solve the following equations simultaneously.
1. 2x + y = 3 and x2 + y + x = y2
2. y = − 6 − 2 and y = − 3x + 2
x + 1
[14]
Solutions- 2x + y = 3 ………………… eqn (1)
x2 + y + x = y2 ………….. eqn (2)
y = –2x + 3 ………….. eqn (3) Use the linear equation (1) to write y alone on one side of the equation.
Substitute eqn (3) into eqn (2), to eliminate the y variable.
x2 + (–2x + 3) + x = (–2x + 3)2 3 Simplify both sides.
x2 – x + 3 = 4x2 – 12x + 9 Factorise the trinomial.
0 = 3x2 – 11x + 6
0 = (3x – 2)(x – 3)
∴ 3x – 2 = 0 or x – 3 = 0
∴ x = 2/3 or ∴ x = 3
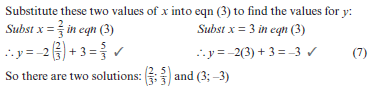 - y = − 6 − 2 and y = − 3x + 2
x + 1
y = − 6 − 2…………………(eqn 1)
x + 1
y = –3x + 2…………………..(eqn 2)
y is alone on one side of both equations.
∴ y = − 6 − 2 = –3x + 2 …………LCD = x + 1
x + 1
∴ –6 –2(x + 1) = –3x(x + 1) + 2(x + 1)
∴ –6 –2x –2 = –3x2 – 3x + 2x + 2
∴ 3x2 – x – 10 = 0
∴ (3x + 5)(x – 2) = 0
∴ x = -5/3 or x = 2
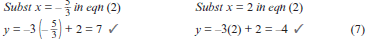
[14] |
Activity 7
- Show that the roots of x2 – 2x – 7 = 0, are irrational, without solving the equation. (3)
- Show that x2 + x + 1 = 0 has no real roots. (3)
- If x = 2 is a root of the equation 3x2 – 5x – 2k = 0, determine the value of k. (2)
- The solutions to a quadratic equation are: x = 5 ± √12 − 3a .
For which value(s) of a will the equation have equal roots. (3) - Determine the value(s) of k for which the equation 3x2 + (k + 2) x + k = 0 has equal roots (4)
[15]
Solutions- a = 1; b = –2 ; c = –7
Δ = b2 – 4ac = (–2)2 – 4(1)(–7)
= 4 + 28
= 32
∴ The roots will be irrational
(Δ > 0 and not a perfect square) (3) - a = 1; b = 1; c = 1
Δ = b2 – 4ac = (1)2 – 4 (1)(1)
= 1 – 4 = – 3
∴ There are no real roots
(Δ < 0 ) (3) - If 2 is a root of the equation, then x = 2. Therefore, we can substitute x = 2 into the equation.
3x2 – 5x – 2k = 0
∴ 3(2)2 – 5(2) –2k = 0
∴ 12 − 10 − 2k = 0
∴ 2k = 2
∴ k = 1 3 (2) - The equation will have equal roots if Δ = 0
Δ = 12 – 3a
0 3 = 12 − 3a
− 12 = − 3a
∴ a = 4 (3) - 3x2 + (k + 2)x + k = 0
∴ a = 3 ; b = (k + 2) ; c = k
∴ Δ = b2 – 4ac
= (k + 2)2 – 4(3)(k)
= k2 + 4k + 4 – 12k
= k2 – 8k + 4
For equal roots the Δ = 0
∴ k2 – 8k + 4 = 0
∴ k = 8± √(–8 ) 2 –4(1)(4)
2(1)
∴ k = 8± √48
2
∴ k = 7,46 or k = –0,54 (4)
[15]
|








